PanX - A Novel and Unique FEA Platform
PanX enables high accuracy thermomechanical simulation and optimization for parts of any size or complexity
PanX is Accurate.
- Resolve fine geometric details
- Model full build plates (location and interaction of parts)
- Achieve high accuracy thermal predictions (loose powder& weighted average interlayer temperature approach)
- Include actual machine process parameters and timing
- Perform high accuracy calibration
PanX is Scalable.
- Model any geometry regardless of size and complexity without having to defeature the part
- Scale computational performance and runtime linearly with model size, as opposed to cubically in traditional FEA tools
PanX is Fast.
- Simulate even the largest and most complex geometries in a small fraction of the actual build time
- Simulate 100x - infinitely faster than legacy FEA tools
PanX is Efficient.
- Most simulations can be run on an engineering laptop (8 cores, 64GB RAM)
- The most complex geometries (e.g. heat exchangers) can be run on engineering desktops (48 cores, 500GB RAM)
25,874,981 Elements
54,806,663 Nodes
206 GB of RAM
48 Core Desktop
160 Hours to Print
14 Hour PanX Solve
Periodic Adaptivity
In addition to being highly parallelized and architected for very low memory consumption, PanX utilizes a novel Periodic Octree Adaptivity scheme which does not require mesh permutations to be generated or stored. Typical adaptive meshing approaches require that these permutations be generated and stored, resulting in prohibitively large memory consumption.
This 600mm tall HX with 300micron thin fins can be easily meshed without having to defeature or homogenize the geometry. The smallest voxels are 200 microns in width and the entire mesh contains ~570M nodes.
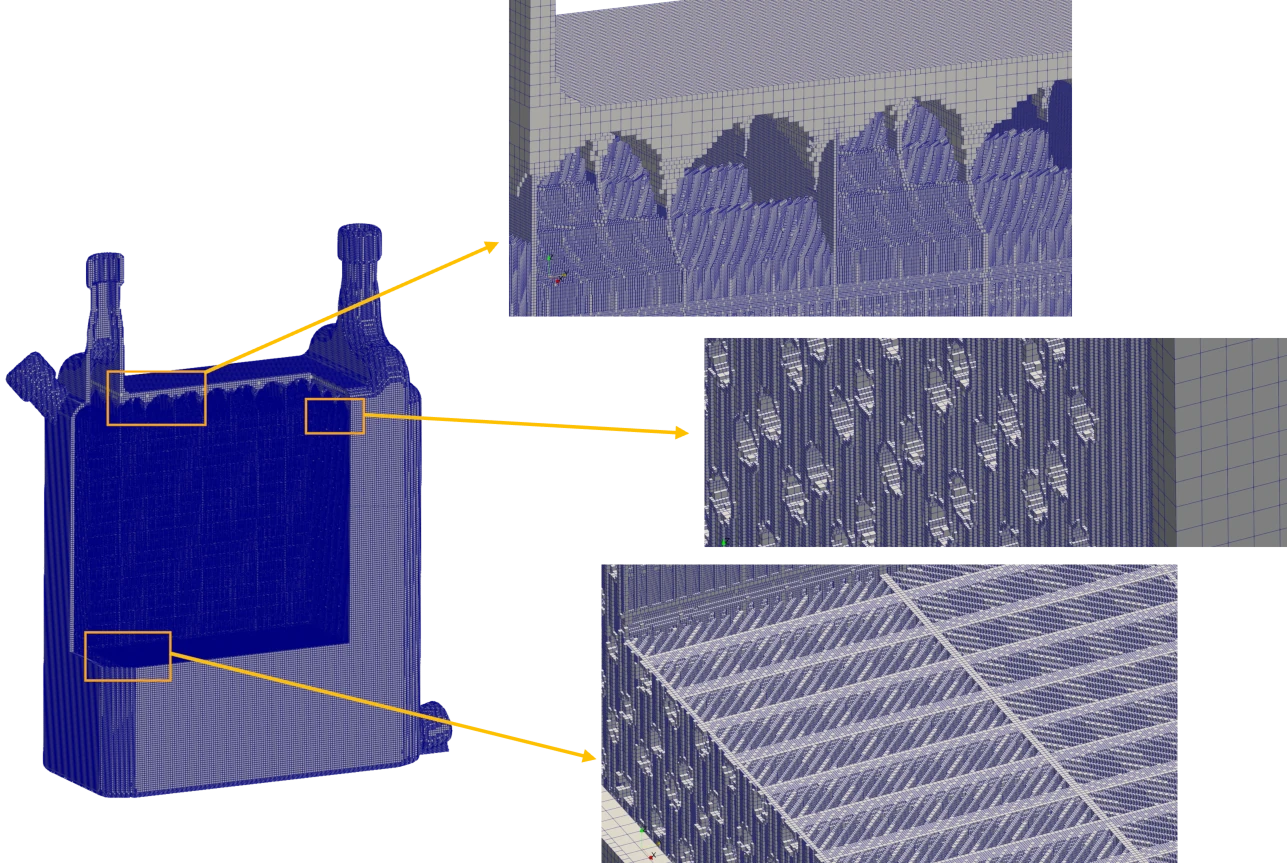
This 600mm tall HX with 300micron thin fins can be easily meshed without having to defeature or homogenize the geometry. The smallest voxels are 200 microns in width and the entire mesh contains ~570M nodes.
Feature Aware Meshing
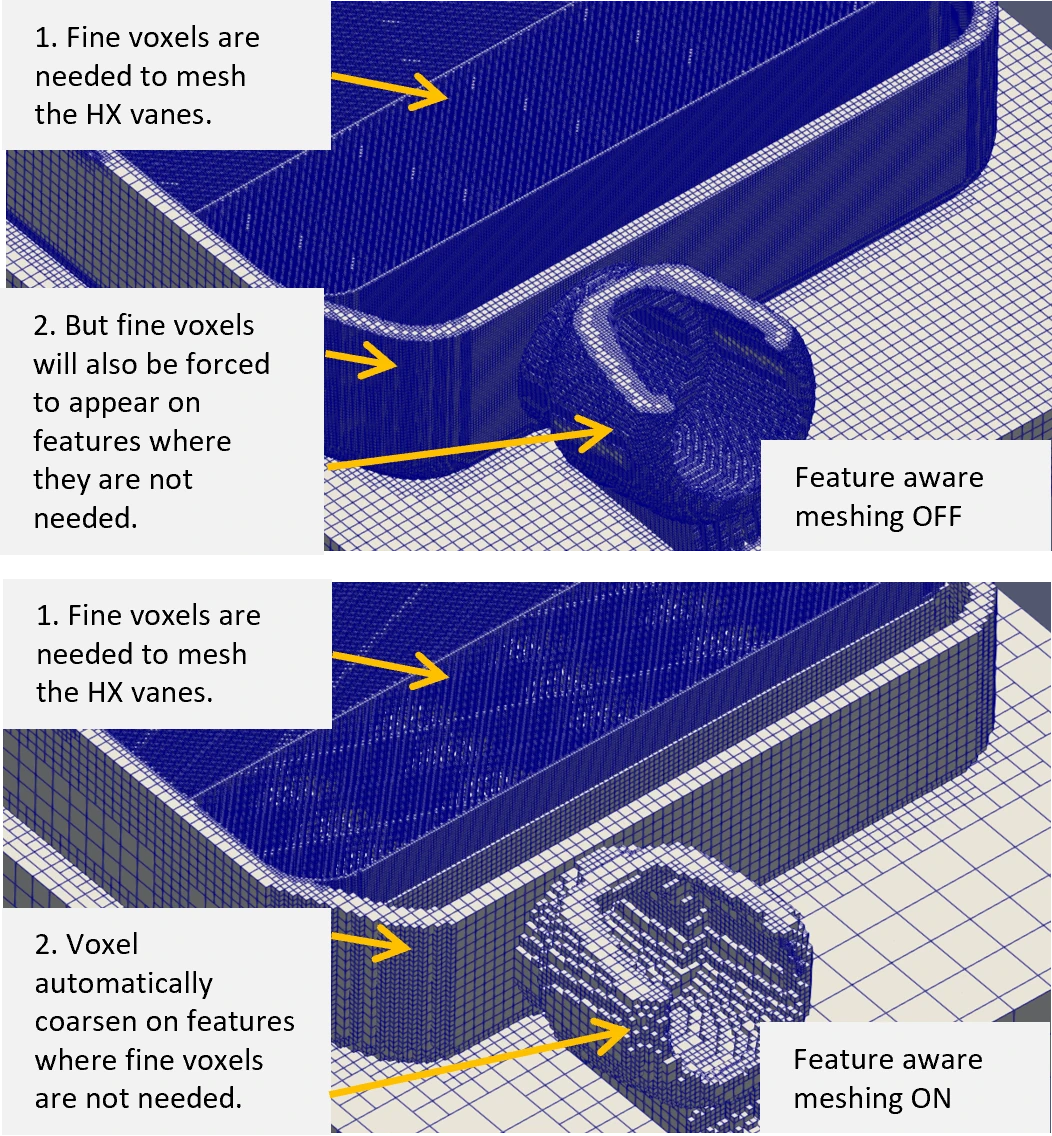
Traditional octree-based voxel meshing results in overly fine finite element meshes. The smallest voxels needed to resolve fine geometric features will also be forced to appear anywhere in the geometry that does not perfectly align with the voxel grid.
Feature-aware meshing solves this issue by determining the size of each geometric feature and allowing for a small error in the meshed geometric representation of the part, in exchange for achieving additional mesh coarsening. Now, fine features can be meshed with small voxels without the fine voxels also appearing elsewhere in the geometry. Here, the approach reduces the node count from over 32M to under 700k.
Multi-Grid Modeling
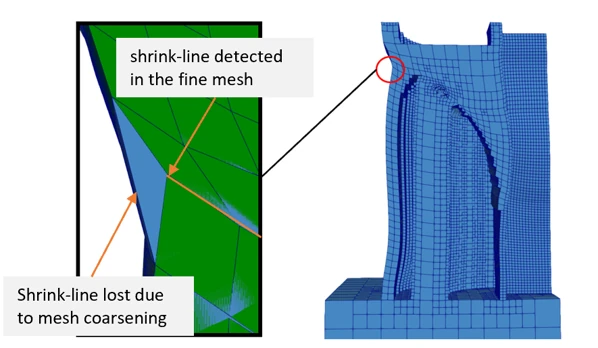
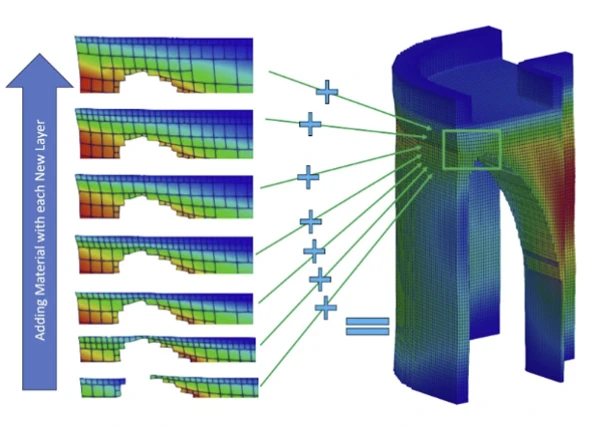
Traditional adaptive mesh coarsening techniques result in large accuracy penalties. Each time a coarsening generation occurs, details (shrink-lines, stress concentrations, etc.) are lost. This is a major challenge for FEA in general, not just AM simulation.
MGM solves the challenge of accuracy loss due to mesh coarsening. MGM solves the thermomechanical problem on a series of transient adaptive meshes. Information from the transient solutions are combined onto a fine resolution result. The result on the fine-grid solution will be nearly identical to the result if the model were run with no mesh adaptivity at all.
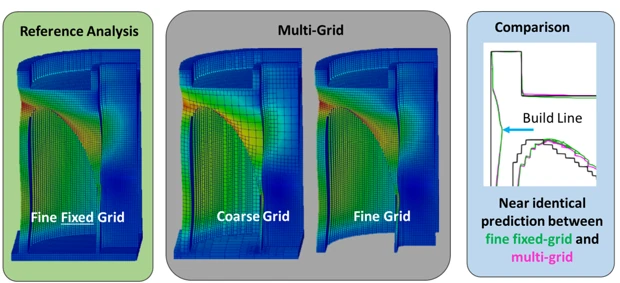
A verification comparing the results of the MGM approach to a refence analysis performed on a static-uniform voxel mesh shows that the MGM approach yields a nearly identical distortion prediction (within 3% of the reference).
MGM solves the challenge of accuracy loss due to mesh coarsening. MGM solves the thermomechanical problem on a series of transient adaptive meshes. Information from the transient solutions are combined onto a fine resolution result. The result on the fine-grid solution will be nearly identical to the result if the model were run with no mesh adaptivity at all.
A verification comparing the results of the MGM approach to a refence analysis performed on a static-uniform voxel mesh shows that the MGM approach yields a nearly identical distortion prediction (within 3% of the reference).
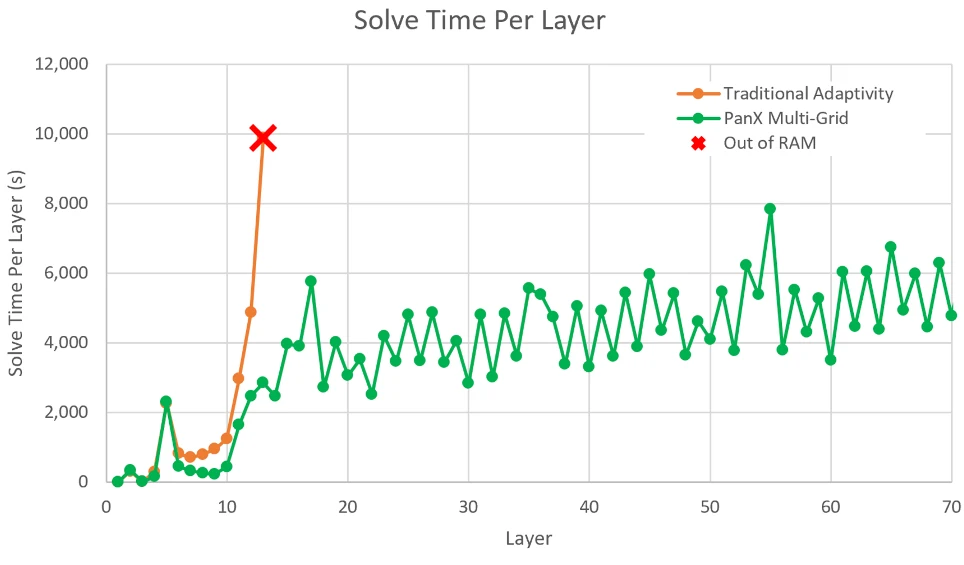
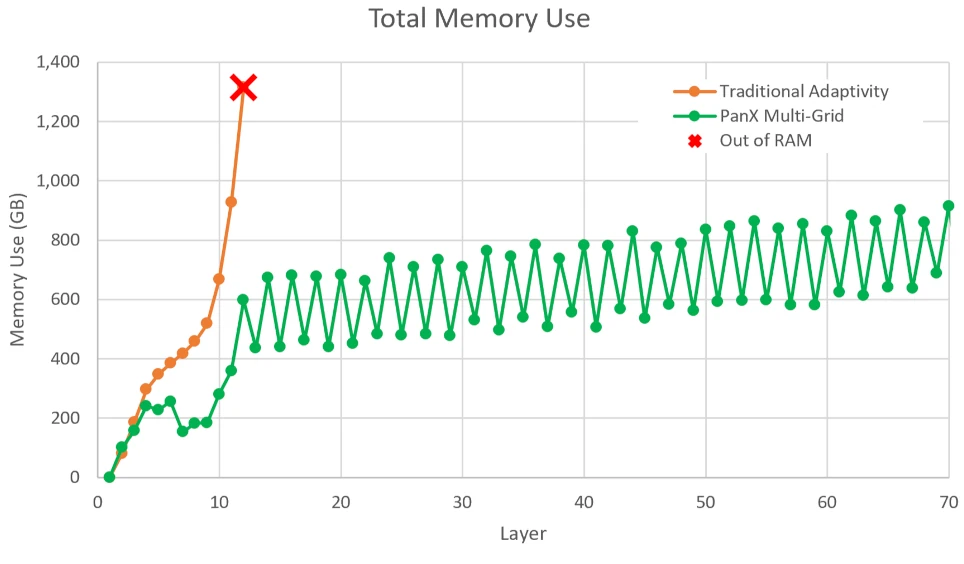
Linear Scaling
The computational performance (runtime & memory requirements) of FEA models scales cubically with problem size. This means that as problems become larger, they quickly become unsolvable even with immense computation resources.
The Multi-grid Modeling approach does not face this limitation and can scale roughly linearly with problem size, allowing for even the tallest components to be solved on and engineering desktop.
The Multi-grid Modeling approach does not face this limitation and can scale roughly linearly with problem size, allowing for even the tallest components to be solved on and engineering desktop.
Accurate Thermal Modeling
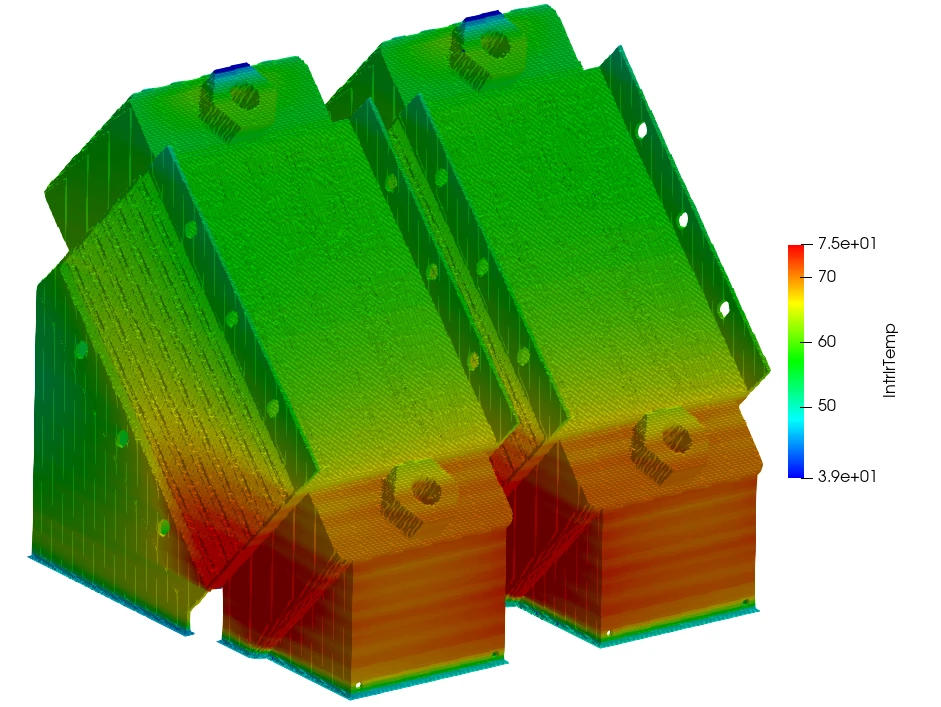
PanX uses a novel “weighted average” approach to simulating the thermal response of the build. The result is high accuracy thermal predictions that are extremely insensitive to spatial and temporal discretization. Because PanX is so computationally efficient, it is also possible to include loose powder in simulations of even the largest build volumes, a critical requirement for accurate thermal modeling.
Multi-Mode Calibration
Novel multi-mode calibration approach allows for calibration of inherent strains for in-plane and out of plane distortion modes as well as thin and thick sections. Because PanX accounts for thermal strain and plate level effects at the part scale, the need for endless calibration (e.g. building many calibration samples at different locations and/or temperatures) is eliminated.
PanX calibration approach eliminates the need to input temperature dependent material properties or other unknowns such as laser absorption efficiency.
Account for Machine Processing Conditions
To further improve model accuracy, PanX can input machine parameters on a voxel-by-voxel basis, allowing users to account for spatially varying parameters.
PanX can also import and account for exact machine process timing, resulting in dramatically improved thermal predictions.
PanX can also import and account for exact machine process timing, resulting in dramatically improved thermal predictions.
Account for Toolpath Direction
Typical inherent-strain based tools do not produce accurate results for DED processes since they rely on an assumptions that the scan direction rotates between layers and that the deposition is 2.5 axis (planar).
PanX reads in G-Code to determine toolpath directionality and sequencing. The directionality allows for different applied plastic strains to be applied in the longitudinal and transverse directions of each weld bead, and the sequencing allows for correct activation of material even for 6-12 axis systems. These innovations allow for extremely fast and accurate simulation of part-scale DED.
PanX reads in G-Code to determine toolpath directionality and sequencing. The directionality allows for different applied plastic strains to be applied in the longitudinal and transverse directions of each weld bead, and the sequencing allows for correct activation of material even for 6-12 axis systems. These innovations allow for extremely fast and accurate simulation of part-scale DED.
Crack Risk
Stress and/or strain predictions from FEA are not useful for assessing crack risk because as the FE mesh is made finer, those predicted results converge toward the analytic solution of infinity near any geometric concentration. This is a major issue for the entire field of local damage modeling, not just in AM.
PanX solves the stress/strain singularity problem using P-integrals, a mesh-independent criteria for crack propensity.
PanX solves the stress/strain singularity problem using P-integrals, a mesh-independent criteria for crack propensity.
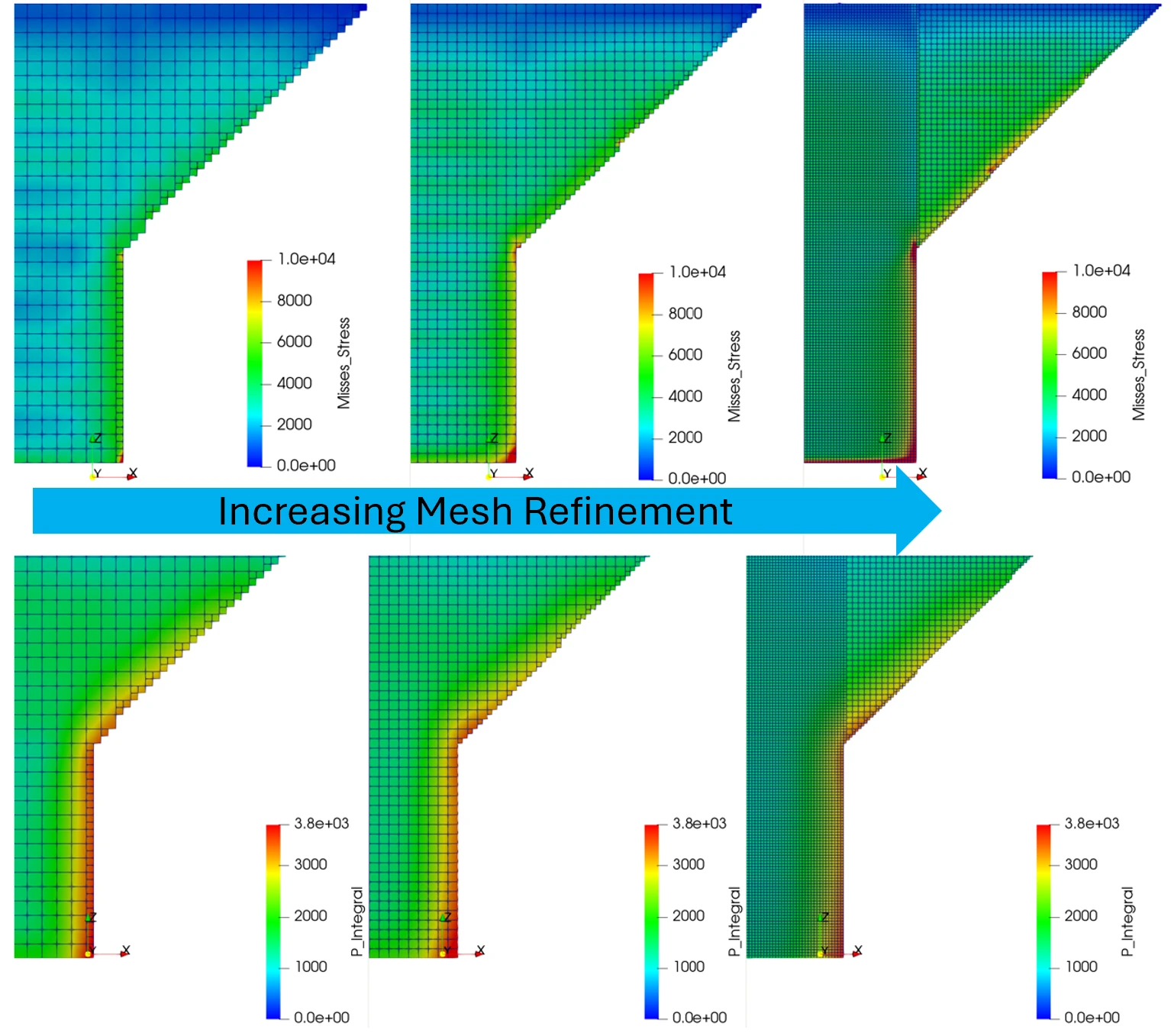
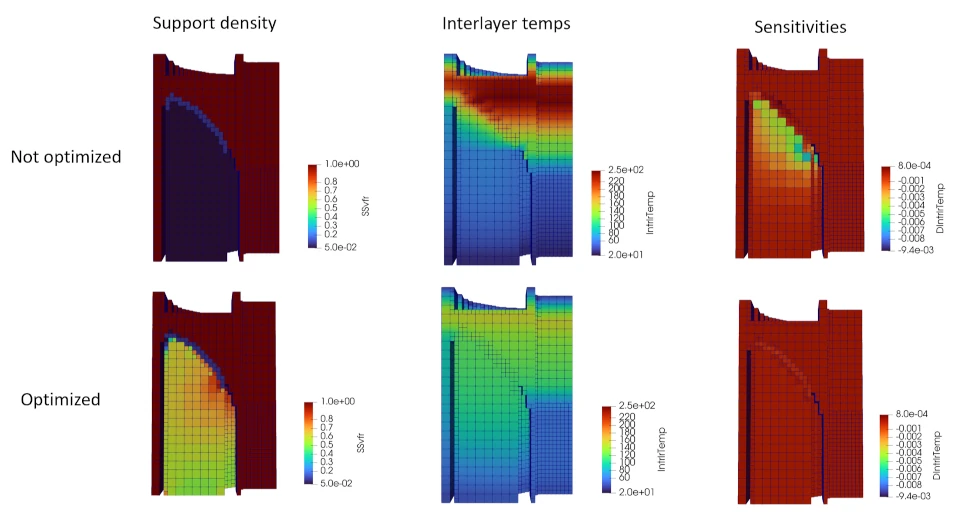
Gradient-based Optimization (under development)
PanX computes adjoint sensitivities to drive efficient optimization (effectively topology optimization for the build process). In this example the constraint is to keep interlayer temperatures below a threshold and the objective is to minimize support volume. The density of every element in the support volume is a design variable. The optimization converges in 8 iterations and takes only a total of 31 seconds on an 8-core laptop.